Statics, Trigonometry, Probability, Number System, Series, Arithmetic Progression ,Geometric Progression etc 

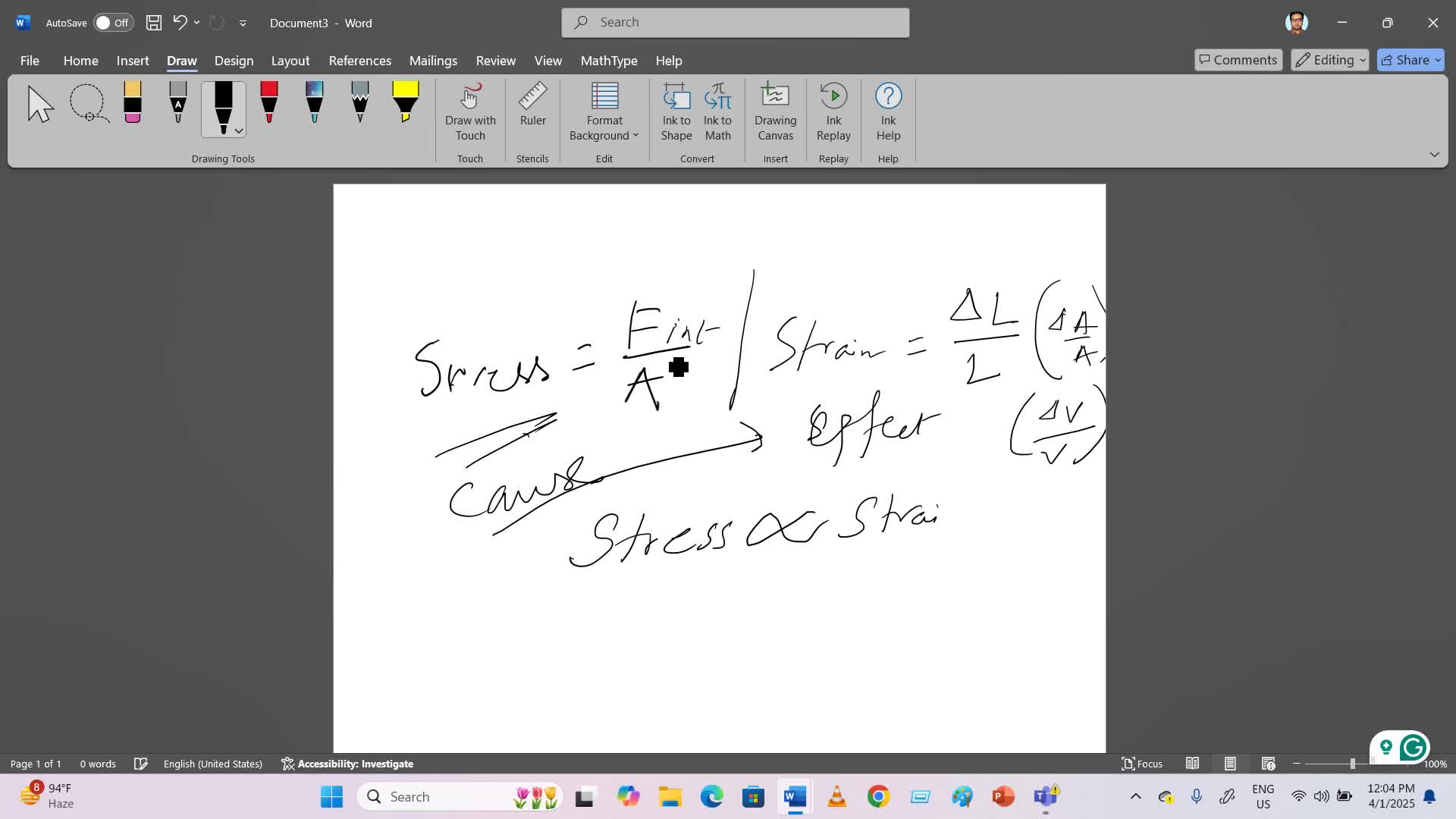
1. Statics

• Usually relates to physics, focusing on forces in equilibrium.
• In mathematics, it might refer to static equations or principles in mechanics, involving calculating forces, moments, and equilibria.

2. Trigonometry

• Studies relationships involving angles and lengths in triangles.
• Key concepts: sine, cosine, tangent, their ratios, identities, and applications in solving triangles, waves, and oscillations.

3. Probability

• Concerns the likelihood of events occurring.
• Basic concepts include experiments, outcomes, events, probability formulas, independent and dependent events, and probability distributions.

4. Number System

• Foundation of mathematics dealing with different types of numbers: natural, whole, integers, rational, irrational, real, and complex numbers.
• Operations, properties, and number representations (like decimal, fractions, and surds).

5. Series

• Sequences of numbers following a pattern that can be expressed using formulas.
• Applications include calculating sums of sequences, often used in algebra and calculus.

6. Arithmetic Progression (AP)

• A sequence where each term is obtained by adding a fixed number (common difference) to the previous term.
• Formulae: an=a+(n−1)dan=a+(n−1)d and sum of n terms: Sn=n2(2a+(n−1)d)Sn=2n(2a+(n−1)d).

7. Geometric Progression (GP)

• A sequence where each term is obtained by multiplying the previous term by a fixed ratio.
• Formulae: an=arn−1an=arn−1 and sum of n terms: Sn=arn−1r−1Sn=ar−1rn−1 (for r≠1r=1).