What is Dynamic Programming?

Dynamic Programming, DP in short, is an intelligent way of solving a special type of complex problems which otherwise would hardly be solved in realistic time frame.

What is that special type of problems? 

DP is not best fit for all types of complex problems, it is well suited for the problems with following characteristics only:

1. The given problem must be decomposable in multiple smaller sub problems with similar nature.
2. Sub problems must also be decomposable into still sub problems and this nesting should continue till a stage arises when the current sub problems could be solved with least cost.
3. At any particular stage, the sub problems must be interdependent.
4. At any specific stage the problem could be solved by solving its sub problems.

So this is like Divide and Conquer. Isn't it?

Wait. Don't jump into any conclusion right now. We have not studied the DP procedures yet! we are currently studying the nature of DP problems only. So it will be too early to compare Divide and Conquer with DP.

But this is true, that just a mere look at the characteristics of DP problems gives a feeling that DP is close to Divide and Conquer. But there is a MAJOR difference, in Divide and Conquer, at any stage, the sub problems enjoy No Inter-Dependencies.

Let us put this on hold. We will revert back to this topic once more only after we have got some experience in DP. But for the time being, take it from me that DP and Divide & Conquer are not same.

Why do not you say how DP works? 

DP works as simple as possible. After the problem is broken down to trivial sub-problems in levels, DP starts solving the sub problems bottom up. Once a sub problem is solved, solution is written down (saved) into a table so that if the same sub problem reappears, we get a ready made solution. This is done in every level.

What is so special about this process?

Yes. It is special. See while you decompose a problems into sub problems, sub problems into sub sub problems and so on, you ultimately reach to a point when you need to solve the same sub problems many a times. And this "many" is not a child's play in real life. Lots of computational resources are unnecessarily spent on this which makes the process sluggish with poor time complexity values. 

With DP you can avoid the re computations of the same sub problems.This will save a lot of time and other computational resources. But there are table look ups for solving reappearing sub problems, and this is not going to offer a bed of roses. This will surely take some time, but with hashing and some other smart alternatives,  table look ups can be made easy. 

Getting out of my head! Show me how DP works with an example. 

 Lets think of Fibonacci series. We know that Fib(n) = Fib(n-1) + Fib(n-2). Hence to compute Fib(4),

Fib(4) = Fib(3) + Fib(2)

          = (Fib(2) + Fib(1)) + Fib(2)

          = ((Fib(1) + Fib(0)) + Fib(1)) + Fib(2)

          = ((Fib(1) + Fib(0)) + Fib(1)) + (Fib(1) + Fib(0))

This could easily be done with Divide and Conquer with recursion. But there will be several call for the trivial case Fib(1) and Fib(0).

But in DP style we can think that

                                                          Fib(4)  ------------------- level 0

                                                   Fib(3) + Fib(2) ------------------ level 1

                                          Fib(2) + Fib(1)-------------------------- level 2

                                 Fib(1) + Fib(0) -------------------------------- level 3

 There will be only two calls of Fib(1) and Fib(0) altogether (shown in violet at level 3). The second Fib(1) (shown in red at level 2) will not be called at all as the result of that is already with us. Similarly Fib(2) (shown in green at level 1) will not be called at all as it has already been computed at level 2. In this way we could avoid re-computations in two occasions.

This is the strength of DP. This strength seems trivial with this trivial example, but as the problem size will grow, this strength will seem to have prominent advantage.  Just Think of fib(100)

Is Dynamic Programming a process to find solution quicker?

Yes it is, but the nature of the solution we are talking to is an optimal solution not the exact one. The principle of optimality applies if the optimal solution to a problem always contains optimal solutions to all subproblems . Take the following example:

Let us consider the problem of making N Rupees with the fewest number of Rupee coins.

Either there is a coin of value N Rupees (Exact Solution), or the set of coins making up an optimal solution for N Rupees can be divided into two nonempty subsets, n₁ Rupees and n₂ Rupees (Optimal Solution).

If any of the n₁ Rupees or n₂ Rupees, can be made with fewer number of coins, then clearly N can be made with fewer coins, hence solution was not optimal.

Tell me more on Principle of Optimality:

The principle of optimality holds if

Every optimal solution to a problem contains optimal solutions to all subproblems

The principle of optimality does not say

If you have optimal solutions to all subproblems then you can combine them to get an optimal solution

Example: If we have infinite numbers of coins of 1cents, 5 cents, 10 cents only then optimal solution to make 7 cents is 5 cents + 1 cent + 1 cent, and the optimal solution to make 6 cents  is 5 cents + 1 cent, but the optimal solution to make 13 cent is NOT 5 cents + 1 cent + 1 cent + 5 cents + 1 cent

But there is a way of dividing up 13 cents into subsets with optimal solutions (say, 11 cents + 2 cents) that will give an optimal solution for 13 cents. Hence, the principle of optimality holds for this problem.

Let us see one example where Principle of Optimality does not hold.

In the following graph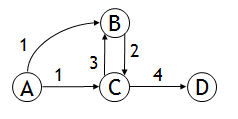

The longest simple path (path not containing a cycle) from A to D is A->B->C->D. However, the sub path A->B is not the longest simple path from A to B (A->C->B is longer)

The principle of optimality is not satisfied for this problem. Hence, the longest simple path problem cannot be solved by a dynamic programming approach.

Can you give me a thorough example of DP? 

Why not! Following is an example of working of Dynamic Programming. It presents a comparative analysis of working of DP with the working of Divide & Conquer.

Let us consider the Coin Counting Problem. It is to find the minimum number of coins to make any amount, given a set of coins.  

If we are given with a set of coin of 1 unit, 10 units and 25 units, then to make 31, how many minimum numbers of coins are required?

Let us check whether the greedy method will work or not. Greedy Method says that just choose the largest coin that does not overshoot the desired amount. So at the first step, we will take one coin of 25 units and then successively in each of next six steps, we will take one 1 unit coin. So ultimately the solution of Greedy Method is 31 = 25 + 1 + 1 + 1 + 1 + 1 + 1 (Total 7 nk!umbers of coins needed)

But evidently there is better solution like 31 = 10 + 10 + 10 + 1 (only 4 numbers of coins are needed). 

Hence Greedy Method will never work.

Now let us check whether any better algorithm exists or not! What about the following?

To make K units:

If there is a K unit coin, then that one coin is the minimum

Otherwise, for each value i < K,

Find the minimum number of coins needed to make i units

Find the minimum number of coins needed to make K - i units

Choose the value of i that minimizes this sum

 Yes. This will work. This is actually following Divide & Conquer Principle but there are two problems with this. This solution is very recursive and it requires exponential amount of work to be done.

 Now, if we fix the given set of coins as 1, 5, 10, 21, 25 and if the desired amount is 63, then the previous solution will require solving 62 recursive sub problems. 

What If we think to choose the best solution among?

•   One 1 unit coin plus the best solution for 62 units
•   One 5 units coin plus the best solution for 58 units
•   One 10 units coin plus the best solution for 53 units
•   One 21 units coin plus the best solution for 42 units
•   One 25 units coin plus the best solution for 38 units

In this case, we need to solve only 5 recursive sub problems. So obviously, this second solution is better than the first solution. But still, this second solution is also very expensive. 

Now let us check how DP can solve it!

To make it shorter in length, let us think that desired value is 13 units and the set of coin given is 1 unit, 3 units, and 4 units.

DP solves first for one unit, then two units, then three units, etc., up to the desired amount and saves each answer in a table (Memoization). Hence it goes like

For each new amount N, compute all the possible pairs of previous answers which sum to N

For example, to find the solution for 13 units,

First, solve for all of 1 unit, 2 units, 3 units, ..., 12 units

Next, choose the best solution among:

• Solution for 1unit   +   solution for 12 units
•  Solution for 2 units   +   solution for 11 units
•  Solution for 3 units   +   solution for 10 units
•  Solution for 4 units   +   solution for 9 units
•  Solution for 5 units   +   solution for 8 units
•  Solution for 6 units   +   solution for 7 units

This will run like following:

There’s only one way to make 1unit (one coin)

To make 2 units, try 1 unit +1 unit (one coin + one coin = 2 coins)

To make 3 units, just use the 3 units coin (one coin)

To make 4 units, just use the 4 units coin (one coin)

To make 5 units, try

• 1 unit + 4 units (1 coin + 1 coin = 2 coins)
•  2 units + 3 units (2 coins + 1 coin = 3 coins)
•  The first solution is better, so best solution is 2 coins

To make 6 units, try

•  1 unit + 5 units (1 coin + 2 coins = 3 coins)
•  2 units + 4 units (2 coins + 1 coin = 3 coins)
•  3 units + 3 units (1 coin + 1 coin = 2 coins) – best solution

Etc.

Ok. I got it but how could you say that computationally this is the best?

The first algorithm is recursive, with a branching factor of up to 62. Possibly the average branching factor is somewhere around half of that (31). So the algorithm takes exponential time, with a large base.

The second algorithm is much better—it has a branching factor of 5. Still this is exponential time, with base 5.

The dynamic programming algorithm is O(N*K), where N is the desired amount and K is the number of different kinds of coins. 

So I don’t hesitate to say that computationally, DP algorithm works best among these threes.

What is this Matrix Chain Multiplication Problem?

Suppose we have a sequence or chain A₁, A₂, …, A_n of n matrices to be multiplied. That is, we want to compute the product A₁A₂…A_n. Now there are many possible ways (parenthesizations) to compute the product.

Let us consider the chain A₁, A₂, A₃, A₄ of 4 matrices. Now to compute the product A₁A₂A₃A_4,there are 5 possible ways as described below:

 (A₁(A₂(A₃A₄))), (A₁((A₂A₃)A₄)), ((A₁A₂)(A₃A₄)), ((A₁(A₂A₃))A₄), (((A₁A₂)A₃)A₄)

 Each of these options may lead to the different number of scalar multiplications, and we have to select the best one (option resulting fewer number of Scalar Multiplications)

 Hence the problem statement looks something like:  “Parenthesize the product A₁A₂…A_n such that the total number of scalar multiplications is minimized”

 Please remember that the objective of Matrix Chain Multiplication is not to do the multiplication physically, rather the objective is to fix the way of that multiplication ordering so that the number of scalar multiplication gets minimized.

 Give me one real example:

 Ok. But before I show you one real example, let us revisit the algorithm which multiplies two matrices. It goes like following:

 Input: Matrices A_p×q and B_q×r (with dimensions p×q and q×r)

Result: Matrix C_p×r resulting from the product A·B

MATRIX-MULTIPLY(A_p×q , B_q×r)

1. for i ← 1 to p
2. for j ← 1 to r
3. C[i, j] ← 0
4. for k ← 1 to q
5. C[i, j] ← C[i, j] + A[i, k] · B[k, j]
6. return C

 In the above algorithm, scalar multiplication in line 5 dominates time to compute C Number of scalar multiplications