If the non-parallel sides of a trapezium are equal, prove that it is cyclic.

If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the centre makes equal angles with the chords.

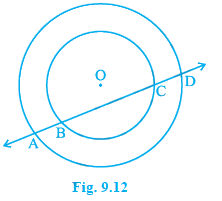
If a line intersects two concentric circles (circles with the same centre) with centre $O$ at $A$, $B$, $C$ and $D$, prove that $AB = CD$ (see Fig. 9.12).

A chord of a circle is equal to the radius of the circle. Find the angle subtended by the chord at a point on the minor arc and also at a point on the major arc.

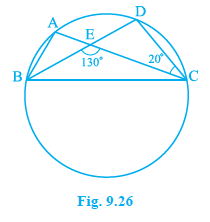
In Fig. 9.26, $A$, $B$, $C$ and $D$ are four points on a circle. $AC$ and $BD$ intersect at a point $E$ such that $\angle BEC = 130^{\circ}$ and $\angle ECD = 20^{\circ}$. Find $\angle BAC$.

$ABCD$ is a cyclic quadrilateral whose diagonals intersect at a point $E$. If $\angle DBC = 70^{\circ}$, $\angle BAC$ is $30^{\circ}$, find $\angle BCD$. Further, if $AB = BC$, find $\angle ECD$.

If circles are drawn taking two sides of a triangle as diameters, prove that the point of intersection of these circles lie on the third side.

Prove that a cyclic parallelogram is a rectangle.

If diagonals of a cyclic quadrilateral are diameters of the circle through the vertices of the quadrilateral, prove that it is a rectangle.

$ABC$ and $ADC$ are two right triangles with common hypotenuse $AC$. Prove that $\angle CAD = \angle CBD$.

Prove that if chords of congruent circles subtend equal angles at their centres, then the chords are equal.

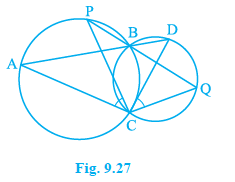
Two circles intersect at two points $B$ and $C$. Through $B$, two line segments $ABD$ and $PBQ$ are drawn to intersect the circles at $A$, $D$ and $P$, $Q$ respectively (see Fig. 9.27). Prove that $\angle ACP = \angle QCD$.

Two circles of radii 5 cm and 3 cm intersect at two points and the distance between their centres is 4 cm. Find the length of the common chord.

If two equal chords of a circle intersect within the circle, prove that the segments of one chord are equal to corresponding segments of the other chord.

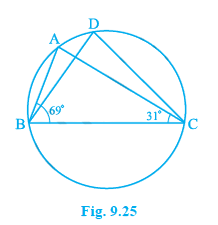
In Fig. 9.25, $\angle ABC = 69^{\circ}$, $\angle ACB = 31^{\circ}$, find $\angle BDC$.

Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?

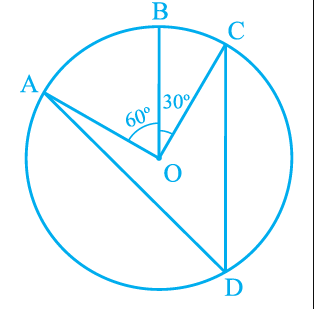
In Fig. 9.24, $\angle PQR = 100^{\circ}$, where $P$, $Q$ and $R$ are points on a circle with centre $O$. Find $\angle OPR$.

A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary each having a toy telephone in his hands to talk each other. Find the length of the string of each phone.

Recall that two circles are congruent if they have the same radii. Prove that equal chords of congruent circles subtend equal angles at their centres.

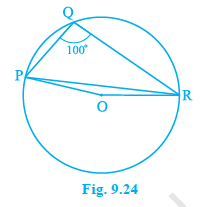
In Fig. 9.23, $A, B$ and $C$ are three points on a circle with centre $O$ such that $\angle BOC = 30^{\circ}$ and $\angle AOB = 60^{\circ}$. If $D$ is a point on the circle other than the arc $ABC$, find $\angle ADC$.